TP n°4 - Additionneur logique
1ère année maturité
Tout le contenu vu durant les TP fait partie entière de la matière à connaître lors d'évaluation.
Vous avez la possibilité de rendre votre TP à la fin des deux périodes pour obtenir une rétroaction sur votre travail.
Objectifs
- Ecrire une table de vérité.
- Définir une équation logique et pouvoir la simplifier.
- Construire un circuit logique à partir d'une table de vérité ou une équation.
- Analyser un circuit logique.
- Comprendre l'addition binaire par un système logique.
Un circuit logique est un montage électronique qui prend des signaux d’entrée (0 ou 1) et donne une ou plusieurs sorties (0 ou 1) selon certaines règles logiques.
- Le 0 représente la valeur logique "FAUX" ou aucun courant électrique
- Le 1 représente la valeur logique "VRAI" ou présence de courant électrique
Ces circuits sont construits avec des portes logiques :
| Nom | Schéma | Opération |
|---|---|---|
| AND | 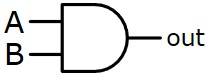 | A·B |
| OR | 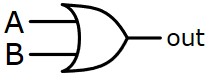 | A+B |
| NOT | 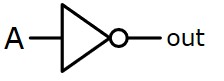 | A |
| XOR | 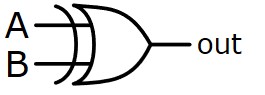 | A⨁B |
Une table de vérité montre toutes les combinaisons possibles d’entrées et la ou les sorties correspondantes du circuit.
Exemple avec une porte AND:
| X | Y | Z |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Voici un circuit logique à 2 entrées et une sortie mais son schéma est inconnu.
Vous pouvez modifiez les entrées de ce circuit pour déterminer la sortie S.
- Ecrivez la table de vérité correspondante.
- Dans le simulateur ci-dessous, construisez le circuit logique qui implémente cette table de vérité. Pas besoin d'écrire dans ce cas d'équation logique.
Lorsqu'on analyse un circuit logique, il peut s'avérer utile d'ajouter des sorties intermédiaires. Ce sont des signaux qui ne seraient pas utilisés directement dans le composant électronique mais qui permettent de simplifier la compréhension des courants électriques internes au circuit.

Dans l'exemple ci-dessus, les sorties I1 et I2 ont été ajoutées afin simplifier le calcul logique pour la porte OR avant la sortie S.
Voici un circuit logique à 3 entrées et une seule sortie Z. Vous ne pouvez pas agir sur les entrées.
Dans le simulateur ci-dessous, il y a un nouveau composant appelé "afficheur" qui va représenter les nombres binaires en nombre entier en base 10. Vous allez apprendre à l'utiliser.
- Par un clic droit sur ce composant, modifiez le nombre de bits d'entrée pour être sur 4 bits.
- Ajouter trois entrées connectées à cet afficheur et assurez-vous que vous arrivez bien afficher le nombre binaire 1111 en décimal.
- Toujours avec clic-droit, vous pouvez essayer de l'orienter autrement, par exemple vers le bas, pour mieux comprendre l'ordre des entrées.
Si on devait simuler un circuit avec des données encodées à l'octet, les entrées ne deviennent pas très pratiques à utiliser vu la place qu'elles prennent. On peut alors les utiliser un autre composant : IN multiple.
- Ajouter un deuxième afficheur sur un octet.
- Ajouter une entrée multiple que vous modifiez sur un octet.
- Reliez correctement toutes les entrées de l'afficheur et testez.
Pour comprendre réellement comment fonctionne un ordinateur avec des portes logiques, prenons le calcul le plus simple: 1 + 1 = 2.
Soit deux nombres A et B codé sur un bit, que va être la table de vérité de l'addition de A et B.
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Constat: Pour additionner deux nombres (A et B) sur 1 bit, il faut une sortie sur 2 bits (C et S). En effet, 1 + 1 = 10(2)
Le nom des sorties n'est pas choisi au hasard: S pour le résultat de la somme des deux bits, et C pour la retenue qui se dit carry en anglais.
- Complétez le circuit logique ci-dessous pour correspondre à la table de vérité ci-dessus, à l'aide de portes logiques.
- Ajouter un afficheur en sortie pour être sûr de votre résultat.
Vous venez de créer le composant électronique que l'on appelle demi-additionneur. Seules deux portes logiques sont nécessaires sont pour simuler une opération arithmétique simple!!
Vous pourrez maintenant l'utiliser dans le simulateur. Mais ceci n'est qu'une étape pour réellement additionner des nombres binaires. Il manque encore une petite étape...
Afin de pouvoir réellement calculer, un ordinateur doit pouvoir additionner des nombres plus grand que 1. Le principe est alors aussi simple que l'addition en colonne que l'on utilise tous en décimal.
Comme vous l'avez appris, pour additionner en colonne, on va additionner depuis la droite les composantes de chaque nombre (A et B) et de l'éventuelle retenue (C), inscrire le résultat en dessous (S). En base 10, si ce résultat et supérieur à 10, on inscrit une retenue (C) sur la prochaine colonne.
En binaire, c'est exactement pareil, comme nous l'avons vu dans la représentation de l'information.
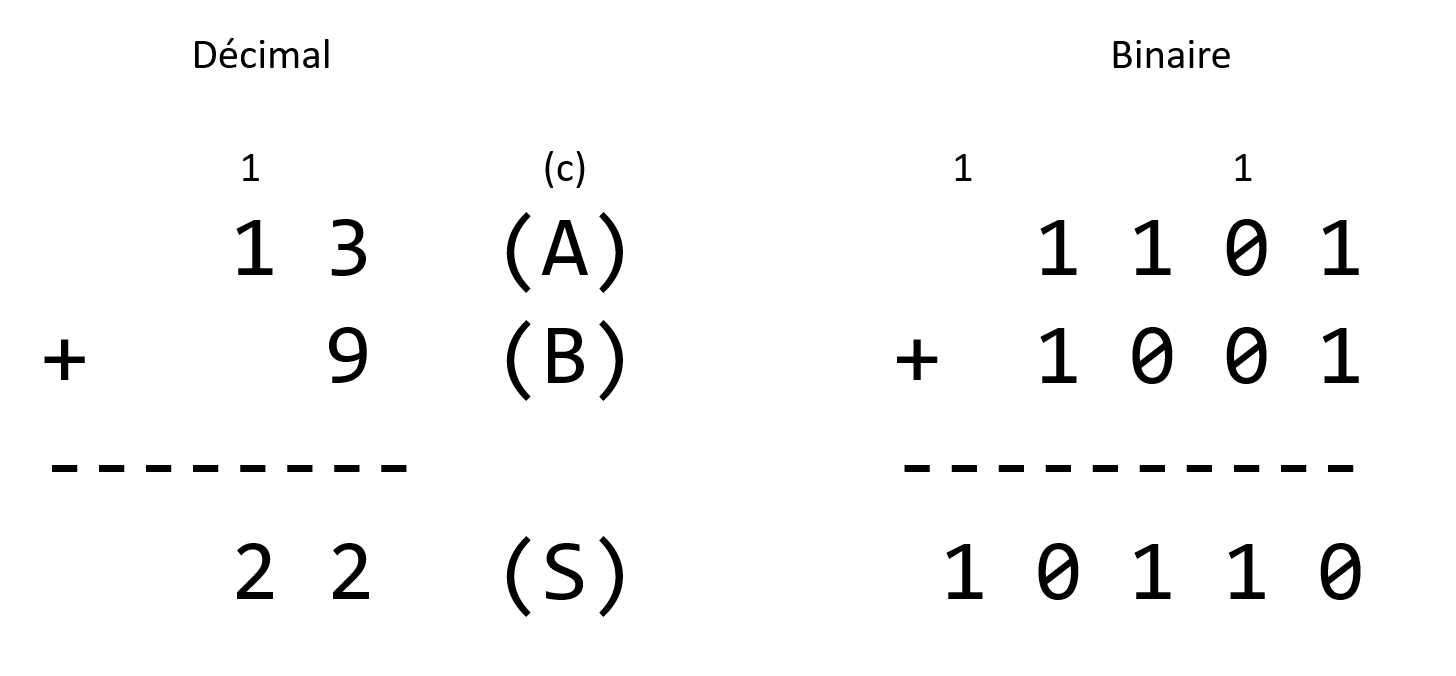
Un composant existe pour effectuer l'addition sur un colonne. Il resemble beaucoup à notre demi-additionneur d'avant, mais on lui ajoute la retenue (Cin) qui est la retenu à prendre en compte dans l'addition de toute la colonne, comme dans la deuxième colonne de l'exemple ci-dessus.
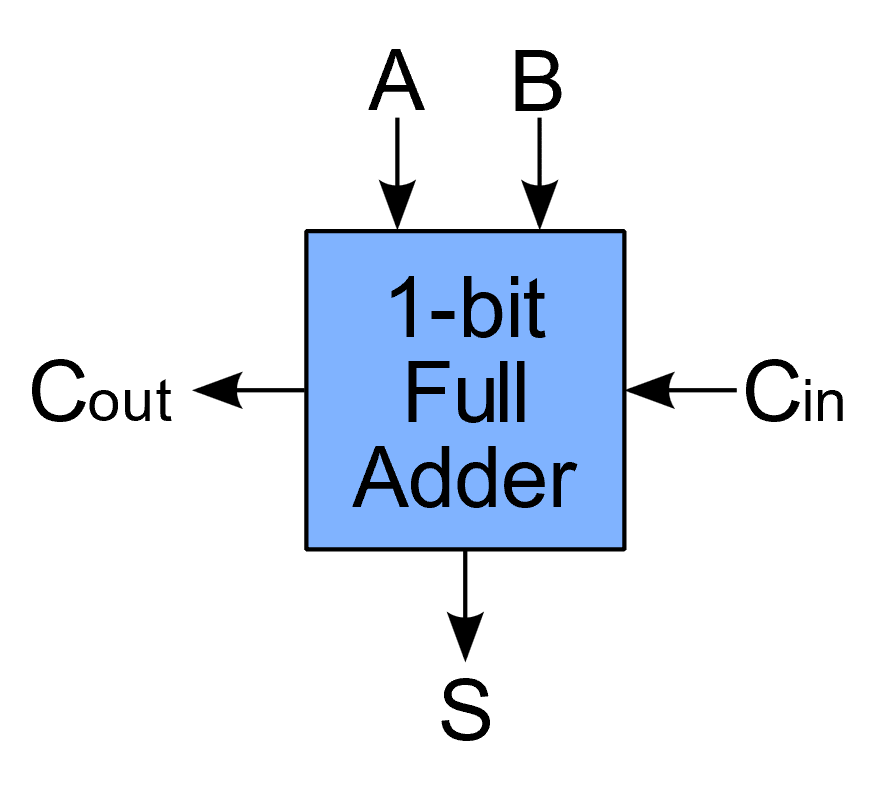
- Que représentent Cout et Cin ?
- Combien d'additionneur faut-il dans un circuit pour additionner des nombres encodés sur 4 bits ?
- Complétez le circuit suivant pour réaliser l'addition sur deux nombres encodés sur 4 bits.
- Combien d'additionneur faudrait-il pour additionner des nombres encorder sur 4 octets comme dans nos processeurs actuels?
5 - 3 = +5 + (-3)
Donc étant capable d'additionner deux nombres entiers non signés, on sait en fait également traiter la soustraction!
Implémentez un circuit logique pour donner la représentation binaire du nombre
négatif en complément à 2.
Observez le bit de poids fort (tout à gauche) à 0 : il ne peut pas être
modifié afin de s'assurer de donner le plus grand positif signé sur 4 bits,
soit 0111(2) = 7(10). Cela est fait grâce à une entrée
normale, et
en vérouillant sa valeur (clic-droit).
En résumé
Pour terminer ce TP, résumez ce que vous avez appris, de la manière que vous préférez (description, carte mentale, schéma, ...).
Pour vous aider, répondez à ces questions.
- Combien de ligne possède une table de vérité à 2, 3 et 4 entrées ?
- Comment écrit-on les entrées d'une table de vérité ?
- Comment simplifie-t-on une équation logique ?
- A quoi servent des signaux intermédiaires ?
- A quoi sert la représentation à 2 et pourquoi l'utilise-t-on ?